3.141592....で始まる無理数π。円周を直径で割っただけのものがこれほどまでに数学に絡んでくるとは、小学校の頃は思ってもみませんでした。今回は、（一部の！？）人々を魅了してやまないπのお話（というより証明）です。πの値が実験によっても算出できることを示したビュフォンの針の問題を説明したいと思います。
この証明は、私が高校時代にやったもので、確率がめちゃくちゃ苦手な私が適当に、直感ばっか使って証明したものです。よって厳密とはいえませんので、概略としてとらえていただければと思います。確率論においての測度の使用すらしらなかったので…。
レベルとしては、途中で、積分が出てきたり、極限の操作らしきものもあるので、表示通り高校程度の微積に自信のある人を想定しています。では、はじめましょう！
ビュフォンの針の問題の内容を以下に示します。
平面上に等間隔で平行線を引き、その間隔の半分の長さの針を投げた時、針が平行線と交わる確率は１/πである
簡単な命題でしょ？あなたが平面上に等間隔で平行線を何本もひいておきます。そして、その間隔の半分の針をたくさん用意しておいて、ランダムにばらまきます。そうすると、その針は1/πの確率で引いておいた平行線と交わってましたということです。
そのまま針のランダムさっていってもちょっと扱いにくいので、針の長さを二等分する点（線分である針を1：1に内分する点。以後針の中点と呼びますましょう。考えるランダムさの一つ目は、針の中点がどこに落ちるか？二つ目は、針の中点が落ちた点を中心とする針の回転分です。つまり、針を投げたら、平面上に落ちて、しばらく針の中点を中心としてルーレットのように回って最終的に止まると考えてください。始めの平面上への落ち方が一つ目のランダムさ、ルーレットの止まり方が二つ目のランダムさということになります。
ところで、針の長さは平行線の間隔の1/2ですから、平行線の間の真ん中らへんに落ちたらルーレットをいくら回しても、平行線と交われません。では、ルーレットがうまく止まれば、平行線に交われるようなある一点に針の中点が落ちた場合(平行線と針の中点の距離が針の長さの半分以下)をまず考えよう。そして、針の中点が平行線に交わることができる場所すべてにわたる確率を合計しよう。最後に、交わられないところに針の中点が落ち場合も考慮にいれる。
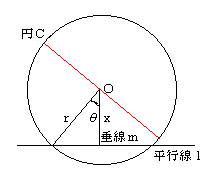針の長さ(２ｒ)を１：１に内分する点をｓ。ｓがある点Ｏに落ちる時、Ｏを中心とし半径ｒの円Ｃを考える(ルーレットの円)。その円Ｃが平行線ｌと交わる時、平行線ｌへのＯからの垂線ｍと、Ｏから円Ｃと平行線ｌの交点への線分がなす角をθとする。また、垂線mの長さをＸとする。
左図参照。赤は針のつもり、これが点Ｏを中心として回転した時の軌跡を円Ｃだとみよ。
x<rであるならば（つまり今考えている状況）針がうまく回れば平行線と交わる。その確率を求めよう。針は円Ｃの直径の一つになるように落ちる。つまり、針のすべての落ち方は針の片方をπ[rad]回転させた分あり、その内、平行線ｌと交わるのは２θ分である。よってその確率は
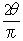
まとめれば、針の中点がx<rに落ちたら、平行線と交わる確率は2θ/π[1]である。
[1]は針の中点が、平行線と交わるようなある点に針が落ちた時の、針と平行線が交わる確率である。針の中点が0<x<rの時、針は平行線と交わりその時の確率は[1]を満たしながら常に変化する。(蛇足だが、xが変われば、当然θが変わるので確率[1]も変わる)。言葉を変えれば、私たちは先ほど、針の中点と平行線との距離xを変数とする平行線との交わる確率の関数を求めたわけである。そして、またこの関数はある点に針の中心が落ちた後の確率であることにも注意しておこう。しかし、我々が求めたいのは落とす前からの確率である。
よって、針が平行線と交わる時(0<x<r)の確率は、（ｓが点Ｏに落ちる確率）×（[1]の確率） のｘ＝０からｘ＝ｒまでの総和である。それは次のようにして求める。
x=rのとき、垂線をｎ個に区切る。その一つの間隔の長さをΔｘと表す。ｓがｎ個ある間隔の内どの１つの間隔に落ちるかの確率は1/nである。しかし、ｎが無限大であるときを考えると、ｓがある一点に落ちる確率もまた同じとしてよい（だろう）。また、どんなｘ（垂線mから針の中心sの距離）もΔｘのｋ個分（ｋは整数）で表すことができる。そうするとｋ＝１からｋ＝ｎまでの（ｓが点Ｏに落ちる確率）×（[1]の確率）の総和が求めたい確率である。積分を使って計算すれば(図参照)
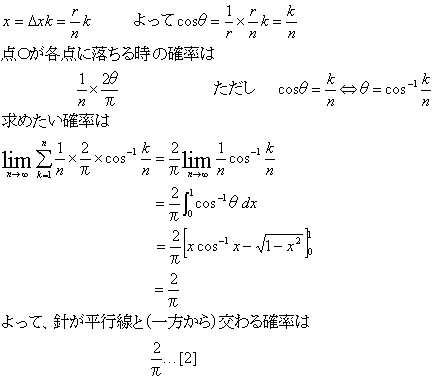
計算の中で、cosの逆関数の積分を用いた。高校レベルで導出するためには、補足を参照のこと。
[2]はｓが平行線ｌと交わることのできる点(0<x<m)に落ちた時の確率である。以上ですべての準備が整った。ここで求めたい確率、つまり針が投げられて後の確率を(針の中点ｓが平行線と交わることのできない点に落ちた場合もあわせて)考えよう。針が投げられてからの挙動を順を追って考えていこう。
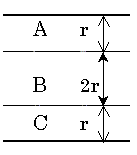
針が投げられて平行線の間隔のどれかの上に針の中点ｓが落ちる確率は1である。それからあと、ｓが落ちる領域を左図のＡ，Ｂ、Ｃに分ける。Ａは上側の平行線からｘ＝ｒまでの領域すなわちここにｓが落ちるということは、上側の平行線と交わることを意味する。Ｂは上側の平行線から距離がｒから３ｒまでの領域であり、Ｂにｓが落ちると針は平行線と交わることはない。ＣはＡと同様。
針の中点sがＡに落ちる確率は1/4、Ｂは1/2、Ｃは1/4である。針が平行線と交わる確率は、Ｂではどの平行線とも交わることはないから確率は０、ＡとＢは[2]の確率に従う。よって
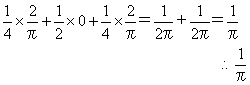
証明終わり
cosxの定義域をうまくとれば、この関数は1対1の関数になり、その範囲で逆関数を考えることができる。cosxの逆関数のことをarccosx、あるいはcos^{-1} x と書く。証明に用いたarccosxの逆関数の積分を求めることにしよう。
arccosx(arcsin,arctanも同様に）は微分するとなじみのある式になることが分かっている。よって、arccosxの積分を求める前に、arccosxの微分をまず求めよう。（なぜそうするのかは後述）
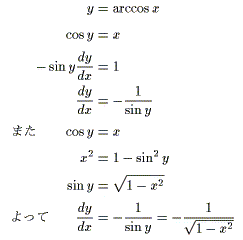
非常になじみのある式がでてきた。ある大学入試などには、三角関数の逆関数(arccosなどなど)の知識があれば簡単に解けそうなものもあった。知っておくといいかもしれない。ところで、積分の公式の中で、微分すると簡単になる式を積分するときに用いるのはなんだろう？…もちろん、部分積分法である。あの公式は微分すると簡単になりそうなやつを積分するときに重宝する。たとえば、logxも微分したら1/xになり簡単に積分できる。だからこそ、1=(x)'と見るのである。（積分公式などはそれぞれに長所がある。どんな場合が有効かを常に意識していれば高校程度の積分は楽になる）では、実際に積分しよう。
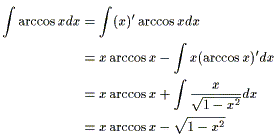
証明の中では、arccosをcosのインバース(-1乗)として書いたが同じこと。積分定数はもちろん省略してある
逆関数などは、教科書の説明を復習すれば分かるとおもう。さらに、数研出版の（1997年度に使っていた）数学Vの教科書には、tanxの逆関数の微分（そう明示していないが）が演習問題として挙げられていた。見ておくとよいと思う。さらに、意欲のある方のために、もっともよい参考書を書いておく。(ページ数は逆三角関数について述べられているところ)